Zahlensysteme

Additionssysteme

”Abzählen”

| = 1, || = 2, |||=3, usw.

Römische Zahlen

I = 1 ll = 2 lV = 4 V = 5 Vl = 6 Vllll = 9 X = 10 Xl = 11 XlV = 14 L = 50 C = 100 D = 500 M = 1000

Stellenwertsysteme

Hexagesimalsystem (Sechziger System)

Basis 60 z.B. Zeit, geografische Längen/Breiten

Duodezimalsystem (Zwölfersystem)

Basis 12 “Ein Dutzend” Vorteil: Restlos Teilbar (2, 3, 4, 6)

Dezimalsystem (Zehnersystem)

Basis 10 → Ursprung Indien, kam über Araber, wird Arabisches System genannt

INFO

Beim Stellenwertsystem ist neben der verwendeten Ziffer auch ihre absolute Position entscheidend für den dargestellen Wert.

Allgemeines Schema für Stellenwertsysteme

Dezimalzahl (Basis 10)

Z(10) =	2	7	8	3	5	Ziffernfolge
	$a_4$​	$a_3$​	$a_2$	$a_1$	$a_0$	Variablen für die Ziffern
	4	3	2	1	0	Stellen
	10⁴	10³	10²	10¹	10⁰	Stellenwert
	10000	1000	100	10	1

konkret: $Z_{(10)}$ = 5⋅$10^0$+3⋅$101^1$+8⋅$10^2$+7⋅$10^3$+2⋅$10^4$ $Z_{(10)}$ = 5⋅1+3⋅10+8⋅100+7+1000+2⋅10000

allgemein:

$Z_{(10)}$ = $a^0$⋅$10^0$+$a^1$⋅$101^1$+$a^2$⋅$10^2$+$a^3$⋅$10^3$+$a^4$⋅$10^4$

Mit der Anzahl der Ziffern : n (hier n = 5)

$Z_{(10)}=\sum i=0n-1=a_i\ast 10^i$

Σ (Sigma) ist das Summenzeichen, in diesem Fall addiert es alle $a_i$ ⋅ $10^i für i gleich 0 bis n−1 ist

Binärzahl (Basis 2)

Die kleinste Informationseinheit ist 1Bit
⇒ 2 Zustände ⇒ 2 Ziffern 0; 1
⇒ Dualzahlen mit der Basis b=2b=2
0≤ai<20≤ai​<2
Die Stellenwerte sind ganzzahlige Potenzen zur Basis b=2b=2

Z(2) =	0	1	1	0	1	1	1	0	Ziffernfolge
	a7a7​	a6a6​	a5a5​	a4a4​	a3a3​	a2a2​	a1a1​	a0a0​	Variablen für die Ziffern
	7	6	5	4	3	2	1	0	Stellen
	2⁷	2⁶	2⁵	2⁴	2³	2²	2¹	2⁰	Stellenwert
	128	64	32	16	8	4	2	1

konkret:

$Z_{10}$ =0∗$2^0$+1∗$2^1$+1∗$2^2$+1∗$2^3$+0∗$2^4$+1∗$2^5$+1∗$2^6$+0∗$2^7$ $Z_{10}$=0∗1+1∗2+1∗4+1∗8+0∗16+1∗32+1∗64+0∗128 $Z_{10}$=2+4+8+32+64 $Z_{10}$=$110_{(10)}$

Hexadezimalsystem (Basis 16)

Hexadezimalzahlen werden mit den Restwertverfahren mit b = 16 berechnet. Sie können allerdings einfacher direkt aus einer Dualzahl ermittelt werden.
Zahlenbasis: 16${}_{(10)}$​=10${}_{(16)}$​
Stellenwerte: …16${}^3$ 16${}^2$ 16${}^1$ 16${}^0$

Dual	Hex	Dez
0000	0	0
0001	1	1
0010	2	2
0011	3	3
0100	4	4
0101	5	5
0110	6	6
0111	7	7
1000	8	8
1001	9	9
1010	A	10
1011	B	11
1100	C	12
1101	D	13
1110	E	14
1111	F	15

$Z(16)$	3	B	2,	A	F
Stellenwert	162162	161161	160160	16−116−1	16−216−2
Z(10)=3∗16${}^2$+11∗16${}^2$+2∗16${}^0$+10∗16${}^{-1}$+15∗16${}^{-2}$
Z(10)=768+176+2+0,625+0,05859375
Z(10)=946,6835938

Umrechnung von Dezimalzahlen >1 (Ganzzahl) in ein beliebiges Zahlensystem

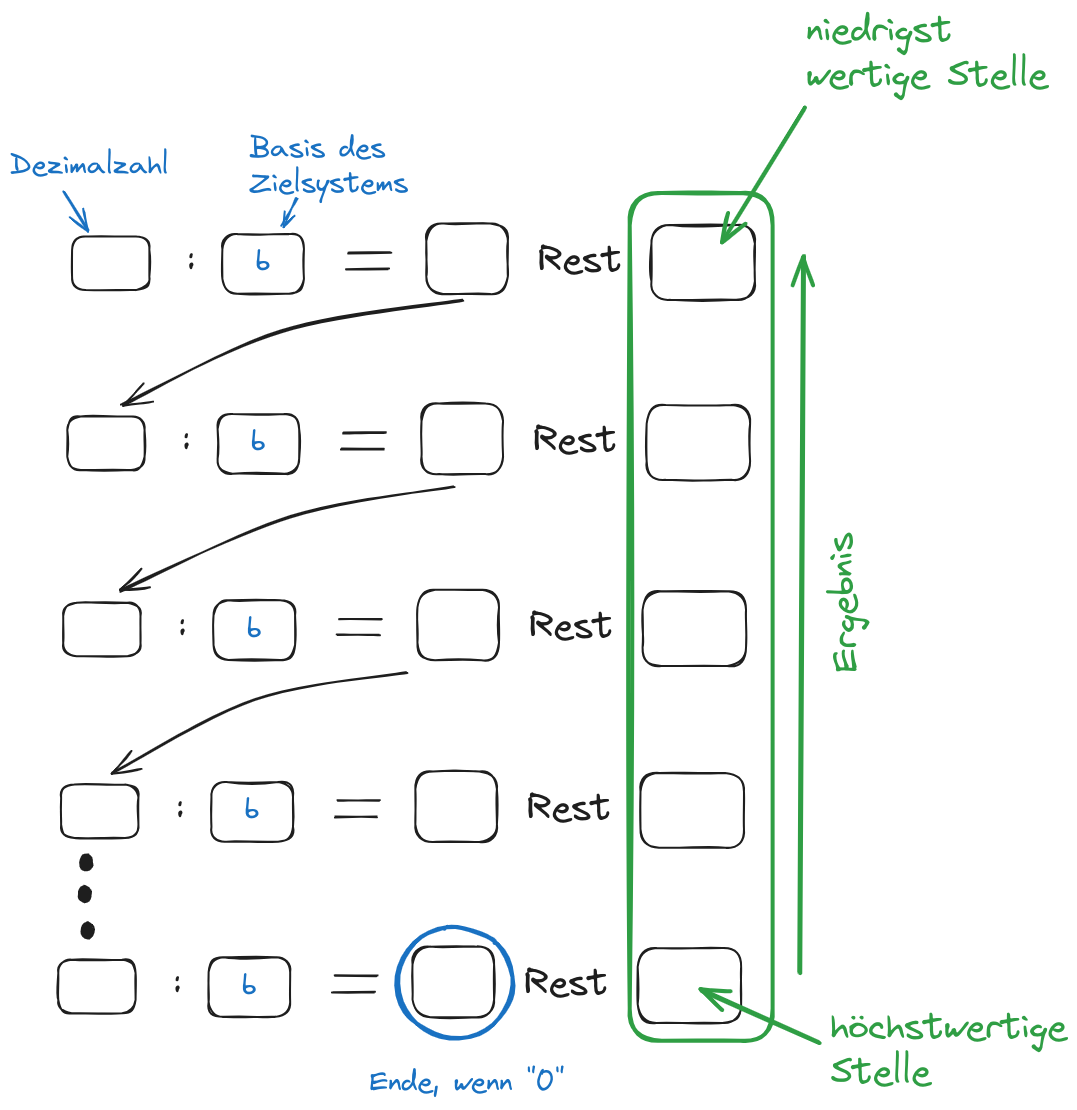
Beispiel Umrechnung in das Binär System 

Gegeben: 154${}_{(10)}$  Gesucht: Z${}_{(2)}$ ⇒ b = 2

Zahl	Rechenzeichen	Basis	Ergebnis	Rest
154	:	2	77	0
77	:	2	38	1
38	:	2	19	0
19	:	2	9	1
9	:	2	4	1
4	:	2	2	0
2	:	2	1	0
1	:	2	0	1

⇒ Z${}_{(2)}$ = 10011010

Restwertverfahren für Zahlen zwischen 0 und 1

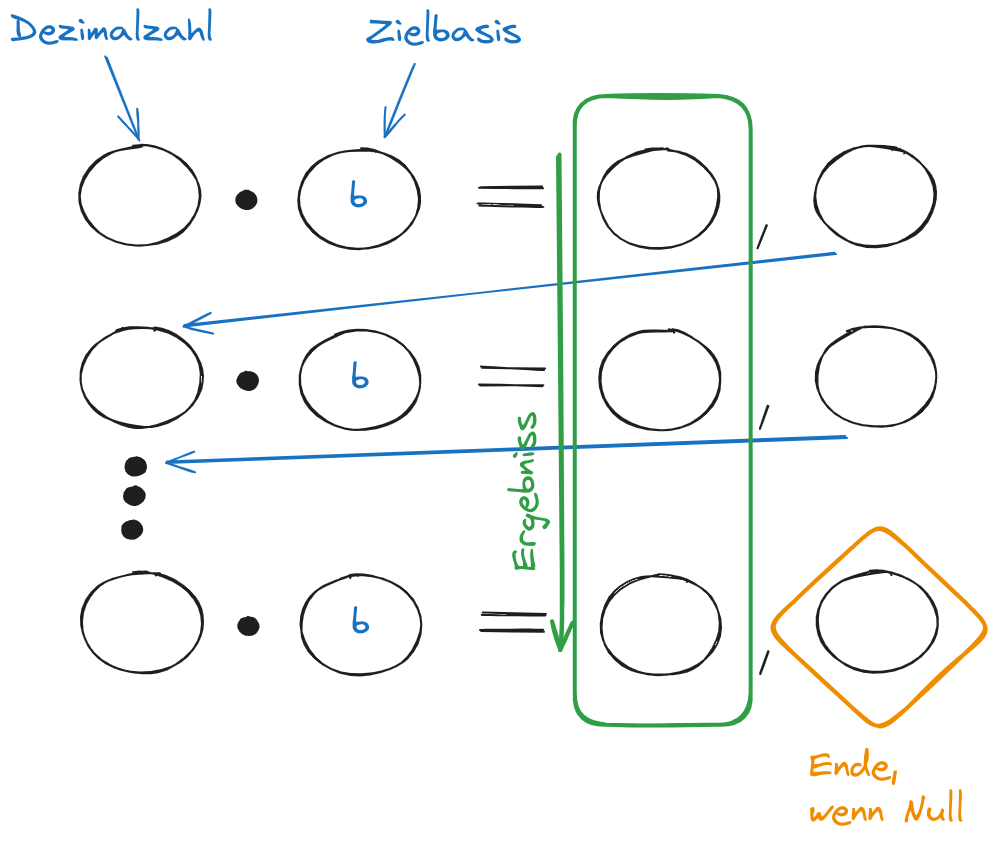Beispiel:

$0,640625_{(10)}=x_{(2)}$
$0,640625\ast 2=1,28125$
$0,28125\ast 2=0,5625$
$0,5625\ast 2=1,125$
$0,125\ast 2=0,25$
$0,25\ast 2=0,5$
$0,5\ast 2=1,0$
⇒ $x_{(2)}=0,101001$

Klärung der Stellenwerte der binären Nachkommastellen 

Die Werte für die Binären Nachkommastellen sind:

2${}^0$	2${}^{-1}$	2${}^{-2}$	2${}^{-3}$	2${}^{-4}$	2${}^{-5}$	2${}^{-6}$	2${}^{-7}$	2${}^{-8}$
1	$\frac{1}{2}$	$\frac{1}{4}$	$\frac{1}{8}$	$\frac{1}{16}$	$\frac{1}{32}$	$\frac{1}{64}$	$\frac{1}{128}$	$\frac{1}{256}$
	0,5	0,25	0,125	0,0625	0,03125	0.015625	0.0078125	0.00390625

$x_{(2)}=0,101001$
$Z_{(10)}=0,5+0,125+0,015625=0,640625$

Merke

Um eine Dezimalzahl in Vor- und Nachkommastellen in einer Dezimalzahl umzuwandeln, müssen die Schritte “Vorkommastellen” und “Nachkommastellen” getrennt ausgeführt werden, danach werden die Ergebnisse zusammengefügt.

• Beispiel:

• $geg.:0,2_{(10)}$ $ges.:x_{(2)}$

  $0,2\ast 2=0,4$
  $0,4\ast 2=0,8$
  $0,8\ast 2=1,6$
  $0,6\ast 2=1,2$
  $0,2\ast 2=0,4$
  ⇒ $x_{(2)}=0,\overline{0011}$

• $get.{:}_{(10)}$ $ges.:x_{(2)}$